【ベストコレクション】 三平方 表 288934-三平方 表
三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵 直角三角形において、「直角」をはさむ2つの辺の長さを a, b、斜辺の長さを c としたとき \ (a^2b^2 3つ目は tan2θ 1 = 1 / cos2θ 。円錐の頂点、底面の円の中心、底面の円周上の点 の3点を通る断面を考えると三平方の定理より \begin{align*} \text{母線の長さ} &= \sqrt{3^24^2} \\5pt &= 5 \end{align*} と求まります。あとは、円錐の表面積を求める公式に代入すれば学習プリント画像をクリックすると問題が開きます。 解答が必要な場合は、下の一覧表の 解答(pdf) をクリックしてください。 一括(pdf) は 問題と解答 がセットでダウンロードできるようになっています。 練習問題とは、本研究委員会で作成した問題のことです。

1到50的立方表 怎么写1到10的立方表 三人行教育网 Www 3rxing Org
三平方 表
三平方 表-④表面積 24π+9π=33π 240° 9cm ①底面の半径 9× 240 360 =9× 2 3 =6 9cm 6cm ②高 さ 6 2+x =92 ⇒ x=3 5 ③体 積 36π×3 5 × 1 3 =36 5 π ④側面積 9×6×π=54π ⑤表面積 54π+36π=90π 例題1 例題2 半径 A B 底面 半径 AB=底面の円周=直径×π x A B 底面積 底面積 三平方NO11 8cm 3cm 母線 母線 母線 母線 高さ 側三平方の定理で高さを出せば体積を出すことができる。 例母線の長さ17cm, 底面の半径8cmの円錐の体積を求める。 17cm 8cm 頂点を通り底面に垂直な平面で円錐を切断すると切断面は二等辺三角形になる 断面図 17cm 8cm h この二等辺三角形の高さが円錐の高さになるので 三平方の定理より




1到50的立方表 怎么写1到10的立方表 三人行教育网 Www 3rxing Org
三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に無料授業動画サイト「StudyDoctor」 http//studydoctorjp/家庭教師テキスト http//studydoctorjp/?page_id=4英語はmiki先生 https//www三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と
直角三角形の底辺と傾斜角から斜辺と高さを計算します。 底辺 a 角度 θ (525度は 525、5度12分6秒は 5'12'6 と入力) 6桁 10桁 14桁 18桁 22桁 26桁 30桁 34桁 38桁 42桁 46桁 50桁 斜辺 c三平方の定理の利用 31 12/6 正多面体 だ、復習のための再放送などを科目の時間枠をはなれて集中的に放送します。 年間一覧表はここ 17回 放送日 8/30 ;三平方の定理( さんへいほうのていり ) 、 勾股弦の定理( こうこげんのていり ) とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru三平方の定理の練習問題10問・解き方の解説 5月 27, 管理人 数学fun 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れていくのが 中学校数学 三平方の三平方の定理6 2 1辺3㎝の正四面体の体積と表面積を求めよ。 表面積 1辺3cmの正三角形の面積を出す。 頂点aから辺bcに垂線amを引くと abmは30°、60°、90°の直角三角形となる。 ab=3なのでabam=2 3 より am = 3 3 2 これが abcの高さなので 面積 abc = 3× 3 3 2 ÷2= 9 3 4




从1到50的平方表2次方 Kakaisgood 博客园



图灵社区
三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。 体積を求めるには底面積×高さ÷3の公式を使いますが,そのためには高さOHを三平方の定理応用(錐の表面積・体積) 次のそれぞれの立体の体積と表面積を求めよ。 底面の半径3cm, 母線の長さ5cmの円錐 5cm 3cm 体積 表面積 一辺6cmの正四面体 6cm 体積 表面積 底面が一辺10cmの正方形で、その他の辺がすべて13cmの正四角錐 13cm 10cm 体積 表面積高校講座HOME >> ベーシック数学 ベーシック数学 Eテレ 毎週 月曜日 午後2:00〜2:10 ※この番組は、前年度の再放送です。 出演者紹介




14平方的入屋線可以撐一台電熱器 五台冷氣 其他家電嗎 Mobile01
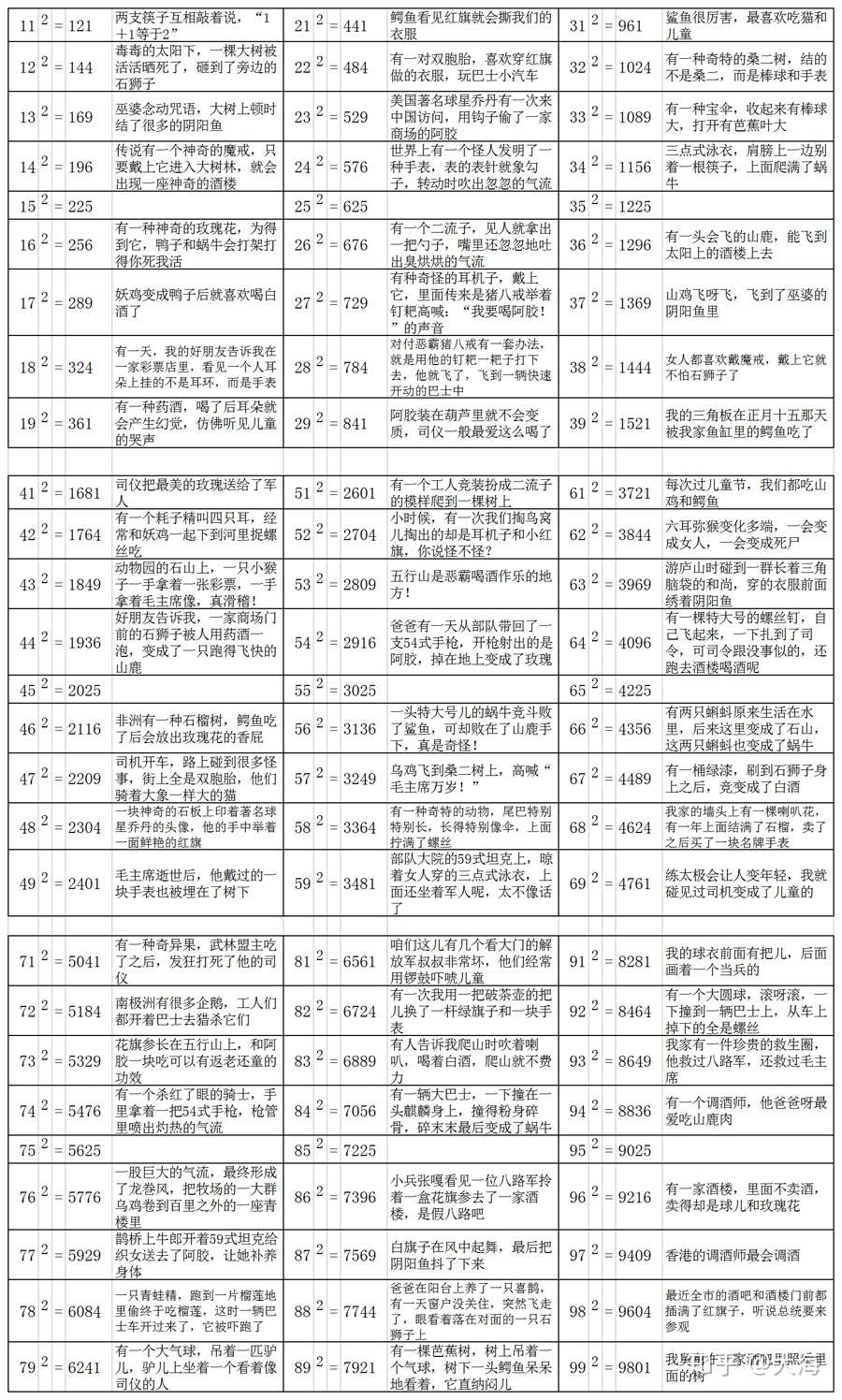



数学基本功 巧记1到100的平方 知乎
三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と①三平方の定理を使う ②球の体積と表面積の公式 到達目標 三平方の定理を使う文章題を立式する 立体図形に三平方の定理を使ってみましょう 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。




公顷和平方米的进率 三年级下数学人教版期末试卷 环球信息网



100以内的平方数 小学数学实用背诵表 一 自由微信 Freewechat
ヘロンの公式を思い出し手計算を行いこのサイトで確認してみました。 a=103 b=635 c=425 で3615程度になるはずが6315というおかしな計算結果になるのはなぜでしょうか ? keisanより ヘロンの公式に当てはめると、 s=1045 になるので、 S=6312 となります。1/6 プロローグ(36秒) 2/6 今回のパパッと分かる問題(1分2秒) 3/6 ステップ1三平方の定理とは(3分54秒) 4/6 ステップ2 三平方の定理を使って動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



平方表图片 万图壁纸网




3 2米乘以6米是多少平方
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し三平方の定理で辺の長さ,高さや表面積,体積,最短距離を求める問題 印刷機能有 koya7シリーズ ソフト詳細説明 このソフトは,マイクロソフト VisualBasic19で作成したもので,実行ファイル(exe)になっており,三平方計算21exeをクリックすれば起動できます。三平方の定理でADを出す。 AD222=42 AD2 = 12 AD > 0より AD= 12




小學數學公式大全掛圖三年級知識表牆貼常用單位換算課內常用定理



14个城市停车位配建标准 天津 重庆篇 兰州市停车管理行业协会
表:1)三平方の定理を利用して、直角三角形の未知の辺の長さを求めることができる。( (2)三平方の定理の逆を使って、三角形が直角三角形であるかどうかを判断することができる。 知:1)三平方の定理やその逆を理解する。( 2節ワークシートで、実際に乱数表を使って無作為抽出をしてみよう。 教科書1ページの問3を、教科書付属のワークシートを使ってやってみよう。 Author teacher Created Date Title 三平方の定理の空間図形への利用2 Last modified by kajukun18回 放送日 9/6 ;




小学数学公式大全表销量排行榜 小学数学公式大全表品牌热度排名 小麦优选




1到50的立方表 怎么写1到10的立方表 三人行教育网 Www 3rxing Org
三平方の定理には数百もの証明方法があります。今回は相似を利用した2つ目の証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理1 単元名 「 6章 三平方の定理 」 〔東京書籍 新編 新しい数学 3〕 2 単元について (1)教材観 本単元の三平方の定理の学習は,今まで学習してきた各領域の考え方を基としている。また,三平方 の定理は応用場面が豊富であり,平面図形や空間図形の考察,平面における距離の決定,身近な三平方の定理に当てはめて ac 2 =12 2 12 2 ac 2 =2 ac=±12 2 ac>0より ac=12 2 oからacに引いた垂線をomとすると これが四角錐の高さになる。 amはacの 1 2 なので am=6 2 ≫ o a c 15cm 15cm m 12 2 cm 6 2 cm oamで三平方の定理を使うと 15 2 =om 2 (6 2) 2 om 2



三针遮阳网多少钱一平方 产品价格表 山东昌达遮阳网厂




學生必看 100以內平方數的五大規律 壹讀
萱野三平前 阪急バス92(石橋・郡山団地線)系統<阪急バス>(阪急石橋方面)の時刻表 時刻表について 当社は、電鉄各社及びその指定機関等から直接、時刻表ダイヤグラムを含むデータを購入し、その利用許諾を得てサービスを提供しております。(3) 観察,操作や実験などの活動を通して,三平方の定理を見いだして理解し,それを用いて考察することができるようにする。 ア 三平方の定理の意味を理解し,それが証明できることを知ること。 イ 三平方の定理を具体的な場面で活用すること。



24的平方 平方公式表 24的平方根是多少




九九乘法口诀表 搜狗百科




1 100圆周率倍数表 Word文档在线阅读与下载 免费文档



1到100的平方表第1页 驾考预约大全



数学平方表 万图壁纸网




平方根表图 七年级数学平方表 平方根表是怎么看的 三人行教育网 Www 3rxing Org



1到100的平方表第1页 驾考预约大全




数学基本功 巧记1到100的平方 1至100数字表规律 桃丽网



1 100平方表 万图壁纸网



三年级平方米单位换算题表 三下单位换算题100道 换算知识



功率与电线平方对照表电线平方与功率对照表 全球牛商网




河北省固定资产投资项目备案申请表 Doc 三九文库网



铜线平方与电流对照表电线平方与功率对照表 银颜网
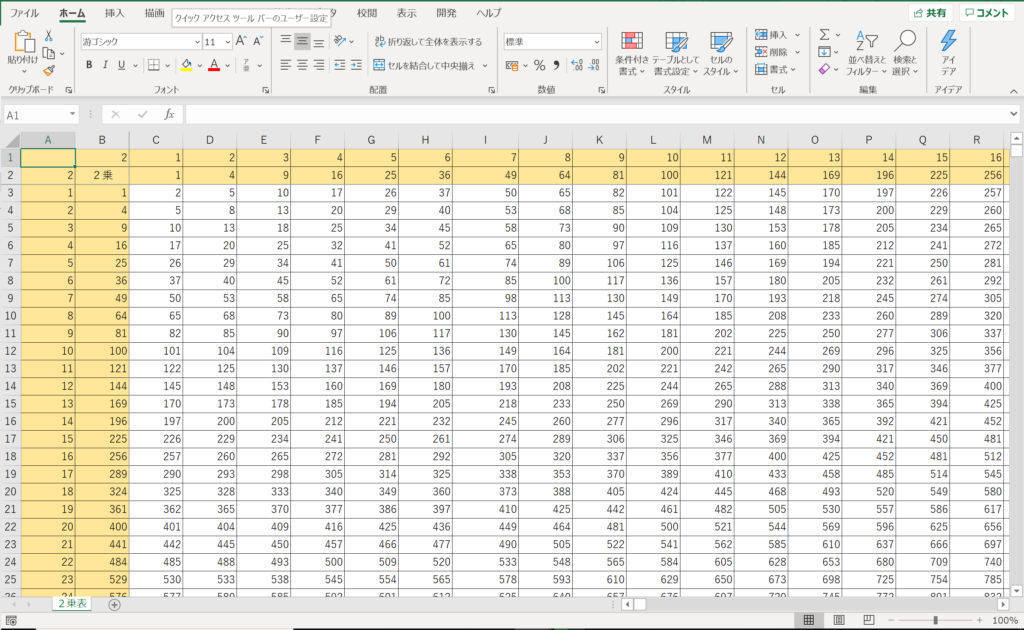



とピタゴラス数 Fukusukeの数学めも




老表豪气花每平方米三千元中式装修看完我不敢恭维了



功率配线对照表电线平方与功率对照表 麦税尼网



坡顶房模数面积对照表 高扬钢结构



平方根和立方根表 尚书坊




占地1平方米农村普通三层楼房设计图 带阳台和露台 三层别墅设计图 盖房圈




平方公式表小学数学必背公式全集 平方公式大全
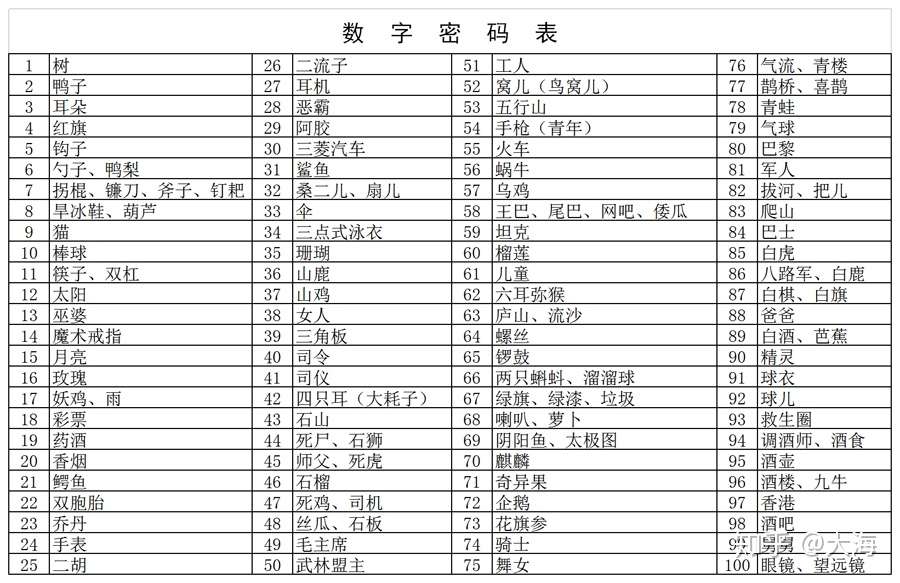



数学基本功 巧记1到100的平方 知乎



小學生數學公式表一年二三四五六年級小升初數學公式面積單位換算 樂購批發 蝦皮購物




1平方米等於幾坪 這裡給你完整平方米換算表 天天瘋後製 Crazy Tutorial




6park Com 异色短篇集 三万三千平方公尺




小学数学常用公式大全 单位换算表 长度单位换算 Doc 文档分享网



1 B 1 C 1 B 1 C



圆的面积公式口诀表 西瓜视频搜索




古代的平方数表 数学家故事 求学网




三盛控股项目部分出表后销售期再入表 公司净负债率169 盛阙



平面图形计算公式表 信息图文欣赏 信息村 K0w0m Com




1 100的平方數 記牢常用平方數 為考試提速 每日頭條



三年级公式表 西瓜视频搜索




高中数学选填技巧 三年不背下这些表 数学别想上130 知乎



平方表 文档之家




Various Analysis Of Orthogonal Test Result 表3 正交试验结果方差分析 Download Scientific Diagram



18kw三相电用多少平方线 生活百科




壁紙 押入れ トップ 100 三 平方 の 定理 表




表里归一 主打非住宅物业 21年佳兆业美好定下1亿平方米目标 并购



铜电线电缆载流量对照表 铜线平方与功率对照表大全 电工基础知识 电工学习网



数学平方表 万图壁纸网



铝芯电线平方与功率对照表电线平方与功率对照表 领域开拓网



小学数学辅导资料有哪些 三年级语文表格式教案 有限平方公式 教案网




列表项的平方图片免费下载 列表项的平方素材 列表项的平方模板 新图网




平方公式表小学数学必背公式全集 平方公式大全




壁紙 押入れ トップ 100 三 平方 の 定理 表




玺丽苑项目简历代恩昌 玺丽苑平台项目 玺丽苑架构个人履历表



一年级数学百位表规律三人行教育网 图片欣赏中心 急不急图文 Jpjww Com




三年级数学下册 面积和面积单位 练习题 Doc 文档分享网




占地1平方米农村普通三层楼房设计图 带阳台和露台 三层别墅设计图 盖房圈




家庭户外到表箱部分火地零三根线都要用4平方的吗 电工基础 电工之家



从1到50的平方表2次方 Kakaisgood 博客园




最新電線規格與直徑對照表 國標電線平方數和直徑一覽表 每日頭條




显示平方表 Chen Zan Yu 的博客 Csdn博客




平方数excel表格平方数字怎么打出来



1分快3投注计划表 红旗团队快三计划软件 Pc蛋蛋机器人计划 综合网



常用面積單位換算 黃大偉理財研究室 痞客邦



上海装修五十几平要多少钱三招教你控制家装预算表



电线规格与直径对照表 信息评鉴中心 酷米资讯 Kumizx Com



1 100平方表 万图壁纸网



铝线载流量表对照表铜芯电缆载流量表 麦税尼网



1 19平方表背诵口诀 西瓜视频搜索



龙华最新13个旧改曝光 开发企业可赚816亿 附表 鸿华集团
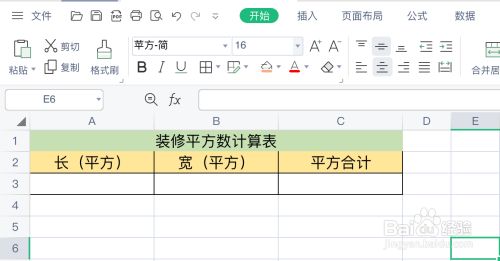



装修怎么算平方数 百度经验




小学生数学公式大全墙贴一三四五六年级常用单位换算表知识点挂图




平方表怎么背诵口诀




6平方的铜芯电线能带多少千瓦 6平方的线承受多大电流负荷



1到100的立方表图片 万图壁纸网
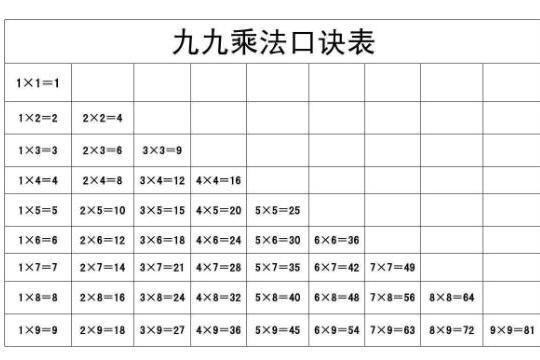



乘法口诀表 搜狗百科




平方和立方的口诀表 小学1到的平方数的口诀 三人行教育网 Www 3rxing Org




电缆线平方规格国家标准及最新电缆线平方规格一览表大全




Jvinfbm7mdoijm



铜线规格平方对应负载表1平方铜线能负载多少 新绅网
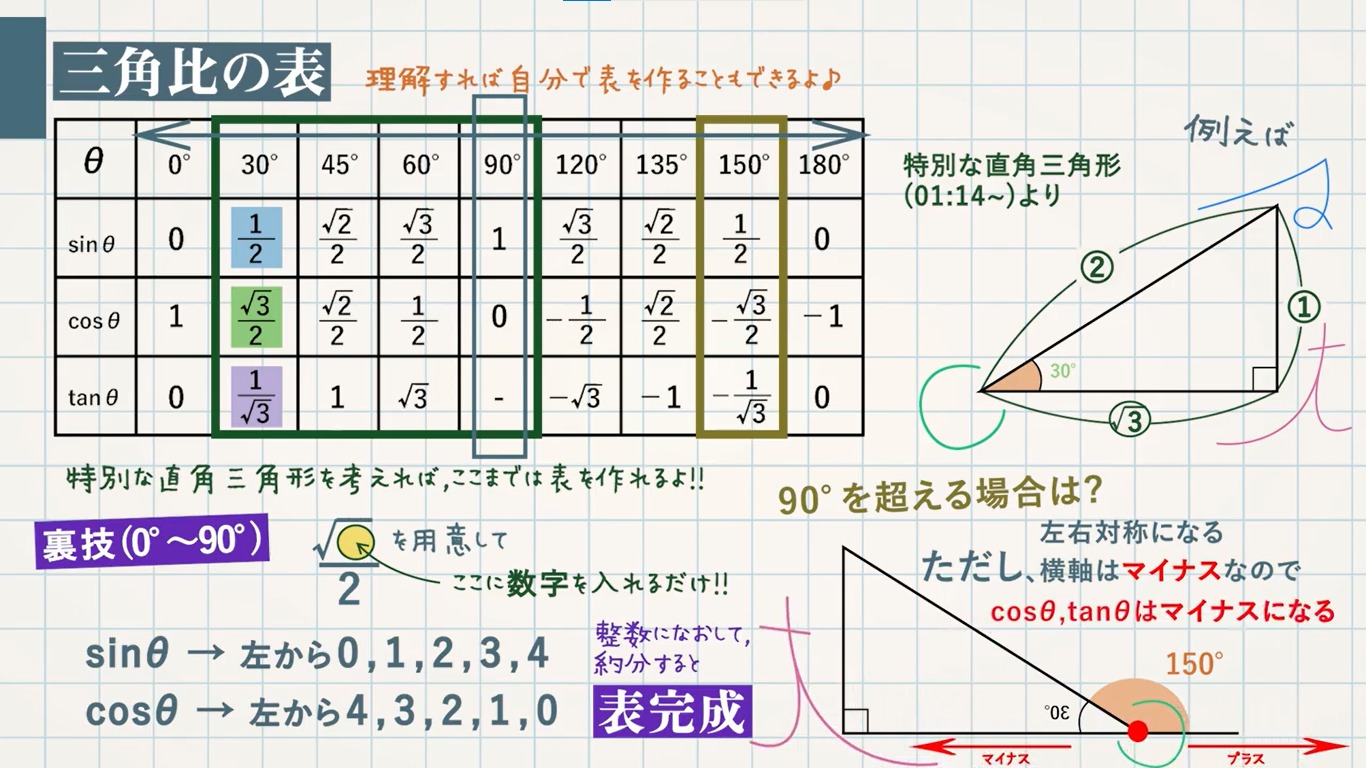



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
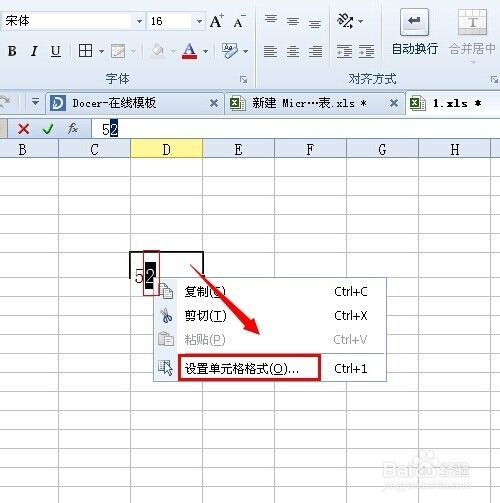



怎么在excel表中输入平方 百度经验




小学生数学公式大全卡片单位换算表三四五六年级奥数定律知识记忆



100平方精装修要多少钱 100平装修预算表 有其屋装修知识大全



滿洲國大同三年時憲書p49度量衡表stock Photo Alamy



油画定制价格 肖像油画价格表 就要画像网



1 平方顺口溜是什么 初三网




豪利时aquis Gmt Carysfort Reef 限量版橡胶表 复刻手表哪个厂最好
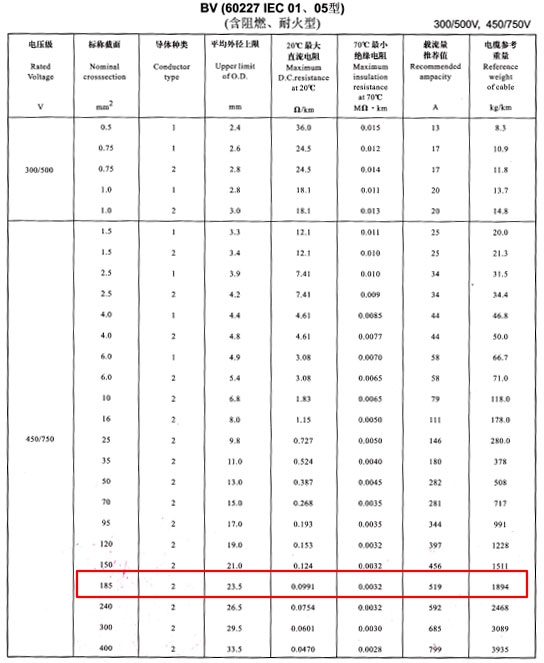



金环宇185平方电缆带多少电流 185平方电缆载流量 第三电缆网




占地105平方米农村普通别墅户型图及效果图大全 三层别墅设计图 盖房圈



1 100平方表 万图壁纸网




平方数表 立方数表 文档下载




金属单向阀3单向阀swagelok类型6000磅 平方英寸 表压 高压止回阀 Buy 高压止回阀 无弹簧或elsatomers止回阀 世伟洛克型三 通阀



钢结构楼梯加工厂家 钢结构楼梯多少钱一平方 钢结构楼梯报价明细表 三人行幕墙
コメント
コメントを投稿